Test de t ou test de Student
D'où provient le test de t
Le test de Student a été publié pour la première fois en 1908 dans la revue Biometrika par William Gosset (1876-1937). Gosset, un chimiste de la brasserie Guinness à Dublin, y avait développé le test de t à des fins de contrôle de la qualité de la production de stout. La compagnie considérait ce test comme un secret industriel. Pour contourner ces règles, Gosset utilisa un pseudonyme, Student, pour publier ce "secret". Ce test est devenu célèbre grâce aux travaux de Ronald Fisher.
À quoi sert le test de t ?
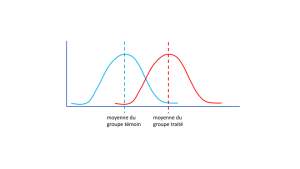
Il permet de vérifier si une différence entre deux groupes n'est pas due à la chance. Si les échantillons proviennent de la même population, on devrait avoir des moyennes qui se ressemblent (accepte H0) et un p > 0.05. Toutefois si notre intervention a eu un effet, nous nous retrouverons avec une différence entre les 2 groupes et un p <0.05 (rejet de H0).
Remarque : Conditions d'utilisation du test de t
Il y a 3 conditions d'application pour le test de t
- La distribution est normale
- La variance des groupes est similaire
- Les valeurs sont indépendantes les unes des autres (parce qu'elles proviennent d'individus différents).
Est-ce qu'il y a une différence entre les deux groupes ? Pour le savoir, nous devons faire un test de t.
Le test de t représente le quotient entre la différence entre les moyennes des groupes / variabilité des groupes.
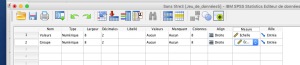
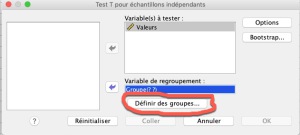
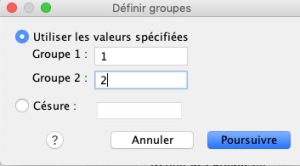
Lorsque nous faisons une comparaison entre deux groupes avec SPSS, il est important de se rappeler que chaque ligne représente un individu. Ainsi si nous avons deux groupes de 10 individus, nous devrions avoir 20 lignes dans une colonne. Dans une deuxième colonne, nous indiquerons à quel groupe l'individu appartient.
Exemple : Exemple de test de t avec SPSS
Vous faites une étude avec 2 groupes de 10 sujets : un groupe témoin (non traité) et un groupe traité (médicament). Vous voulez savoir si votre intervention a un effet sur la variable que vous avez mesurée.
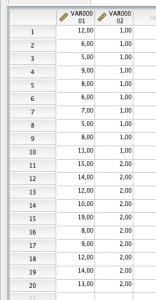
Les résultats sont dans le tableau ci-bas. Les unités de la variable sont en mg/dl Quelle est votre conclusion ?
Témoin | Traité |
|---|---|
12 | 15 |
6 | 14 |
5 | 12 |
9 | 10 |
8 | 19 |
6 | 8 |
7 | 9 |
5 | 12 |
8 | 14 |
11 | 13 |
Comme nous avons dit plus tôt, lorsque nous avons 20 individus, nous devons utiliser 20 lignes dans SPSS. Dans la première colonne nous pouvons mettre les données et dans la seconde indiquer le groupe auquel la valeur appartient.
Vous pouvez identifier le nom des colonnes en cliquant sur vue des variables.
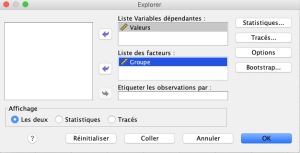
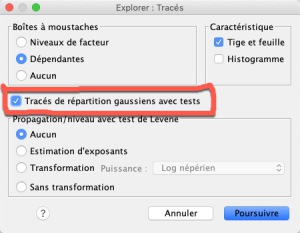
Dans un deuxième temps, nous devons déterminer si les données sont distribuées normalement. Pour ce faire nous utiliserons le test de Shapiro-Wilk. Dans Analyse - Statistiques descriptives - Explorer mettre les colonnes dans les cases suivantes et cliquer sur Tracés...
N.B. Si nous avons deux groupes dans la colonne des données, nous devons le spécifier dans "Liste des facteurs" en ajoutant les groupes dans la case sinon le calcul comprendra les données des 2 groupes. En précisant les groupes, nous aurons les valeurs de distribution pour les groupes individuels.
Dans Tracés, cliquer la case de "Tracés de répartition gaussiens avec tests" - poursuivre et OK
Les résultats apparaîtront plus bas dans le tableau de "Tests de normalité". Nous voyons ici que les données des deux groupes donnent un p > 0.05. Dans ces conditions, on accepte l'hypothèse nulle (les données sont distribuées normalement).
Par la suite, cliquer sur Analyse - comparer les moyennes - Test T pour échantillons indépendants. Mettre les colonnes dans les bonnes cases et cliquer sur "définir les groupes..."
Indiquer les numéros des groupes correspondants. Cliquer sur poursuivre et OK.
Le résultat du test de t apparaîtra dans la fenêtre qui s'ouvrira.
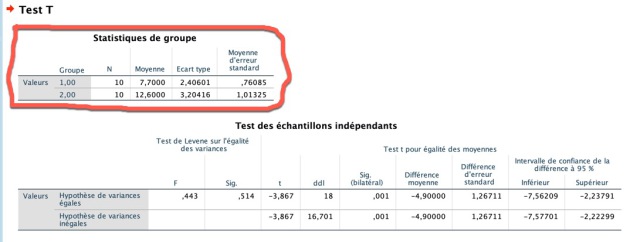
Dans le premier tableau vous trouverez les moyennes et les erreurs-standards de chacun des groupes.
Dans le tableau du bas, vous trouverez le résultat du test pour l'égalité des variances (test de Levene). Le résultat du test nous indique que les variances sont homogènes (égales) p > 0.05. Dans SPSS, pour le test de T, si les variances sont homogènes, nous prendrons le résultat du test de T sur la ligne supérieure. Dans le cas où les variances ne sont pas homogènes, nous prendrons la ligne du bas. Pour notre exemple, nous prendrons la ligne du haut.
Le résultat nous indique un t de -3,867 avec 18 degrés de liberté (nous en reparlerons au prochain cours) et un p < 0.05.
Pour notre exemple la réponse serait : Nous avons effectué un test de t pour déterminer la différence entre nos deux groupes. Dans un premier temps, nous avons déterminé que la distribution pour chacun des groupes était normale (p >0.05) à l'aide du test Shapiro-Wilk. Par la suite, après avoir effectué un test de Levene, pour lequel nous avons constaté que les variances étaient homogènes (p > 0.05). Notre test de t nous indique que la différence entre notre groupe témoin 7.70±0.76 mg/dl et traité 12.60±1.01 mg/dl était significatif (t=-3.87; ddl =18, p < 0.05). Ainsi nous pouvons conclure que le groupe traité présentait une moyenne significativement plus élevée que le groupe témoin.
Remarque : Signe de la valeur de t
Le signe (+ ou -) présent devant la valeur de t est plus ou moins important car tout dépend de ce que l'on place comme premier ou deuxième groupe dans notre analyse. Ainsi vous n'êtes pas obligés de mettre le signe avant la valeur de t.