Écart-type
Écart-type
En anglais: Standard deviation (SD)
Représente la distance moyenne entre chaque donnée et la moyenne de votre échantillon.
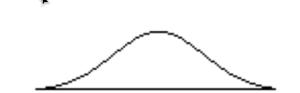
Plus l'écart-type est grand, plus la distance entre chaque point et la moyenne est grande.
Calcul de l'écart-type
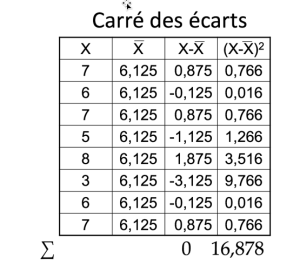
Pour calculer l'écart-type, il faut prendre la différence entre chaque valeur et la valeur moyenne de l'échantillon (6.125 dans notre exemple). Si on additionne toutes ces différences nous arrivons à une somme de 0. Toutefois pour calculer une variabilité, les statisticiens ont pris la valeur individuelle de chacune des différences et ils l'ont mise au carré. Dans ces conditions la variabilité devient un nombre positif. Par la suite la somme de ces différences au carré est divisée par le nombre de valeurs moins 1 (n-1). Dans notre exemple ; 16.878/7 = 2.411. Pour trouver l'écart-type il s'agit de faire la racine carrée de 2.411 = 1.55.
Exemple de calcul pour la variance
Complément : Pourquoi n-1 et non n ?
L'écart-type est une estimation de la déviation standard de la population à partir d'un échantillon...En soustrayant 1 du dénominateur on reste conservateur, car la valeur de notre rapport sera nécessaire plus grande. De plus, plus notre échantillon sera grand, moins l'effet du -1 sera important.
Complément : Pourquoi faire le carré des déviations et la racine par la suite?
- Si nous ne portons pas les différences au carré, la somme des différences sera nécessairement 0 dans tous les cas.
- On veut que les unités de notre écart-type soient les mêmes que notre moyenne. Si on laisse la variabilité au carré, les unités ne seront pas les mêmes que la moyenne
Rappel : Les choses à se rappeler sur l'écart-type
L'écart-type(ET):
- Distance moyenne des valeurs par rapport à la moyenne
- Plus l'ET est grand, plus l'étendue des données est grande
- Sensibles aux extrêmes
Si ET = 0 , il n'y a pas de variabilité ce qui est très très rare et suggère un problème.
Un grand écart-type représente une distribution comme celle-ci
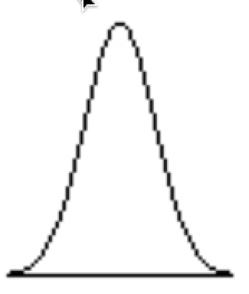
Alors qu'un petit écart-type représente une distribution comme celle-ci
